Notation For All Real Numbers

0.1: Review - Existent Numbers: Note and Operations

Last updated
Save every bit PDF

Page ID: 38205

Real Numbers

Algebra is frequently described equally the generalization of arithmetic. The systematic apply of variables, letters used to represent numbers, allows the states to communicate and solve a broad variety of real-world bug. For this reason, we begin by reviewing real numbers and their operations.

A fixis a collection of objects, typically grouped within braces $\{ \}$, where each object is chosen an element. When studying mathematics, we focus on special sets of numbers.

\[ \brainstorm{align*} \mathbb { N } &= \underbrace{\{ ane,2,3,4,5 , \dots \}}_{\colour{Cerulean}{Natural\: Numbers}}
& W &= \underbrace{ \{ 0 , 1,ii,3,iv,v , \dots \}}_{\color{Cerulean}{Whole\: Numbers}}
&\mathbb{Z} &= \underbrace{ \{\dots ,-three,-2,-1,0,i,2,3,\dots\}}_{\colour{Cerulean}{Integers}} \end{align*}\]

The three periods (…) are called an ellipsis and bespeak that the numbers continue without leap. A subset, denoted $\subseteq$, is a prepare consisting of elements that vest to a given ready. Observe that the sets of naturaland whole numbersare both subsets of the set of integers and nosotros tin can write $\mathbb { Due north } \subseteq \mathbb{Z}$ and $W \subseteq \mathbb{Z}$.

A fix with no elements is chosen the empty set and has its ain special notation:

$\{\:\:\:\}=\varnothing\: \qquad \colour{Cerulean}{Empty\: Set}$

Rational numbers, denoted $\mathbb{Q}$, are defined as any number of the form $\frac { a } { b }$ where a and b are integers and b is nonzero. We tin depict this set using set up note:

$\mathbb { Q } = \left\{ \frac { a } { b } | a , b \in \mathbb { Z } , b \neq 0 \right\} \qquad \color{Cerulean}{Rational\: Numbers}$

The vertical line | inside the braces reads, "such that" and the symbol $\in$ indicates gear up membership and reads, "is an element of." The notation above in its entirety reads, "the set of all numbers $\frac{a}{b}$ such that a and b are elements of the set of integers and b is not equal to zero." Decimals that terminate or repeat are rational. For instance, $0.05=\frac{5}{100}$ and $0.\overline{6}=0.6666…=\frac{2}{three} $.

The set of integers is a subset of the set of rational numbers, $\mathbb{Z}\subseteq\mathbb{Q}$, considering every integer tin can be expressed as a ratio of the integer and i. In other words, whatsoever integer can be written over 1 and can be considered a rational number. For instance, $vii=\frac{7}{one}$.

Irrational numbers are divers equally any numbers that cannot be written equally a ratio of two integers. Nonterminating decimals that exercise non repeat are irrational. For example, $π=3.14159…$ and $\sqrt{two}=i.41421…$.

Finally, the set of existent numbers, denoted $\mathbb{R}$, is defined as the gear up of all rational numbers combined with the set of all irrational numbers. Therefore, all the numbers defined so far are subsets of the gear up of real numbers. In summary,

Figure $\PageIndex{1}$: Existent Numbers

Notation Used to Define Subsets of Existent Numbers

Sets of numbers tin exist described in several ways, including Interval Annotation, Set-Builder Annotation and Inequality Notation.

Interval Annotation

In interval notation, we use a foursquare bracket [ when the ready includes the endpoint and a parenthesis ( to bespeak that the endpoint is either non included or the interval is unbounded.

The smallest number in the interval, an endpoint, is written kickoff.
The largest number in the interval, another endpoint, is written second, and is written after a comma.
Parentheses, $($ or $)$, are used to signify that an endpoint is not included in the interval.
Brackets, $[$ or $]$, are used to bespeak that an endpoint is included in the interval.

Set Note

Another way a set of numbers can be described is inready-builder notation. The braces $\{\}$ are read as "the set of," and the vertical bar $|$ is read as "such that," so we would read $ \{ten|10≤x<30\}$ equally "the gear up of x-values such that 10 is less than or equal to x, and x is less than 30." For a given value of $10$ the statement is either true or faux.

Figure $\PageIndex{2}$ compares inequality notation, gear up-builder notation, and interval notation.

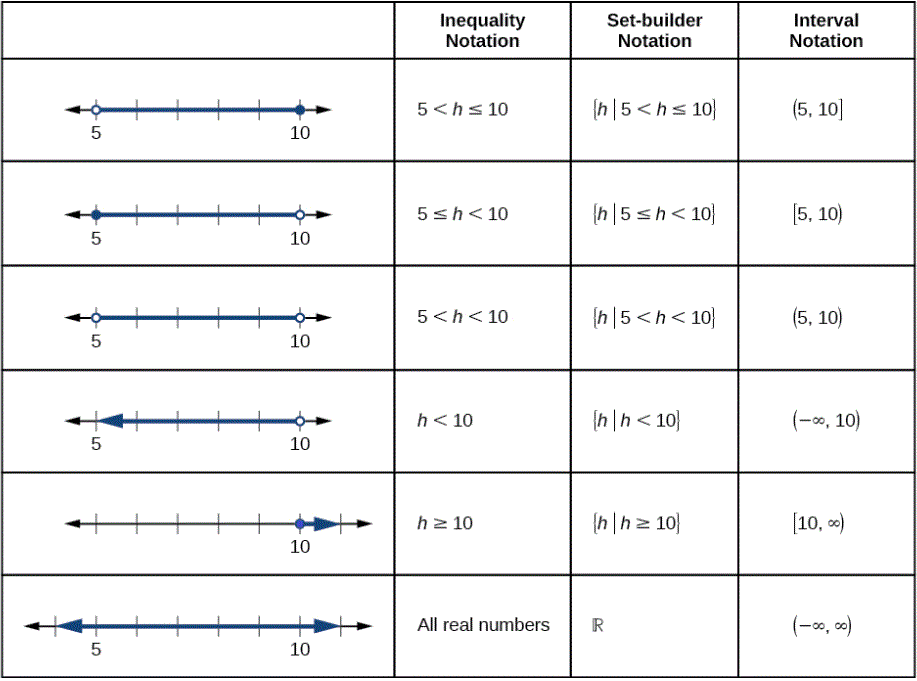
$p.1.1 table1.gif$
Effigy $\PageIndex{2}$: Summary of notations for inequalities, sets, and intervals.

$how-to.png$ How to: Given a line graph, describe the set of values using interval notation.

Identify the intervals to be included in the set up by determining where the heavy line overlays the real line.
At the left finish of each interval, use [ with each finish value included in the set (solid dot) or ( for each excluded stop value (open dot).
At the correct end of each interval, use ] with each cease value included in the prepare (filled dot) or ) for each excluded cease value (open dot).
Utilize the matrimony symbol $\cup$ to combine all intervals into ane set.
Annotation: The word "or" (rather than $\loving cup$) is used to combine sets described by inequalities or Gear up-architect notation.

Compound Inequalities

For sets with a finite number of elements, like for example the sets $\{2,3,5\}$ and $\{5,6\}$, the union of these sets is the fix $\{2,3,v,6\}$. The elements do not have to exist listed in ascending order of numerical value, but if the original two sets have some elements in mutual, those elements should exist listed only once in the union set. The intersection of these two set lists simply those elements common to both sets, $\{v\}$

Wedlock of intervals

There are several different ways to illustrate the spousal relationship of two intervals, which combines all the elements of both sets.

For inequality notation or gear up-builder notation, the discussion "or" is used. (The logical "or" operation requires that either ane or both conditions are true.)
For interval notation, the spousal relationship symbol$ \loving cup $ is used to combine all the elements of both sets.

To find the union of two intervals, use the portion of the number line representing the total collection of numbers in the 2 number line graphs. For example,

Figure $\PageIndex{3}$ Number Line Graph of $ten<3$ or $x\geq 6$

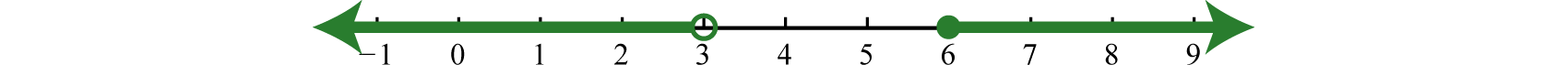
$\color{Cerulean}{Interval notation:}$ $(−∞,3)\loving cup[vi,∞)$

$\color{Cerulean}{Set up notation:}$ $\{10| x<3 \text{ or } x\geq 6\}$

Case $\PageIndex{one}$: Describing Sets on the Real-Number Line

Describe the intervals of values shown on the line graph below using inequality notation, set-builder notation, and interval notation.

[Line graph of $1<=x<=3$ and $5$] — Effigy $\PageIndex{iv}$: Line graph of $ one≤x≤iii \text{ or } x>5 $.

Solution

To draw the values, $x$, included in the intervals shown, we would say, "$x$ is a real number greater than or equal to 1 and less than or equal to 3, or a existent number greater than v."

$ \begin{assortment} {cl}
1≤x≤3 \text{ or }x>5 &\text{Inequality}\\
\{x|1≤x≤three \text{ or } x>v\} \qquad & \text{Set-Builder Notation} \\
[1,3]\cup(5,\infty) & \text{Interval Note} \\
\cease{array}$

Think that when writing or reading interval notation, using a square bracket means the boundary is included in the set up. Using a parenthesis means the boundary is not included in the set up.

$try-it.png$ Try It $\PageIndex{i}$

Given Figure $\PageIndex{five}$, specify the graphed gear up in

words
set-builder annotation
interval note

[Line graph of -ii<=x, -one<=x<3.] — Figure $\PageIndex{5}$: Line graph

Answers: a. Values that are less than or equal to –2, or values that are greater than or equal to –i and less than 3;
b. $\{x|x≤−2 \text{ or } −ane≤ten<three\}$
c. $\left(−∞,−ii\right]\loving cup\left[−ane,3\right)$

Intersection of intervals

There are several different ways to illustrate the intersection of two intervals.

For inequality notation or set-builder note, the give-and-take "and" is used to signify the intersection of two intervals. (The logical "and" operation requires that both conditions must exist true.) The intersection can be more succinctly written as a compound inequality. For case,$−1\leq x$ and $ten<iii$ can exist written more concisely equally $−one\leq x<3$ which reads "negative one is less than or equal to ten and x is less than iii."
When interval notation is used, the prepare composed of only the elements common to both sets is denoted by the intersection symbol, $\cap$.

To observe the intersection of two intervals, accept the portion of the number line that the two number line graphs have in common.

Example $\PageIndex{2}$:

Graph and give the interval notation and set notation equivalent to $x<3$ and $10\geq −ane$.

Solution

Determine the intersection, or overlap, of the two solution sets to $x<iii$ and $x\geq −i$. The solutions to each inequality are sketched above the number line every bit a means to determine the intersection, which is graphed on the number line below.

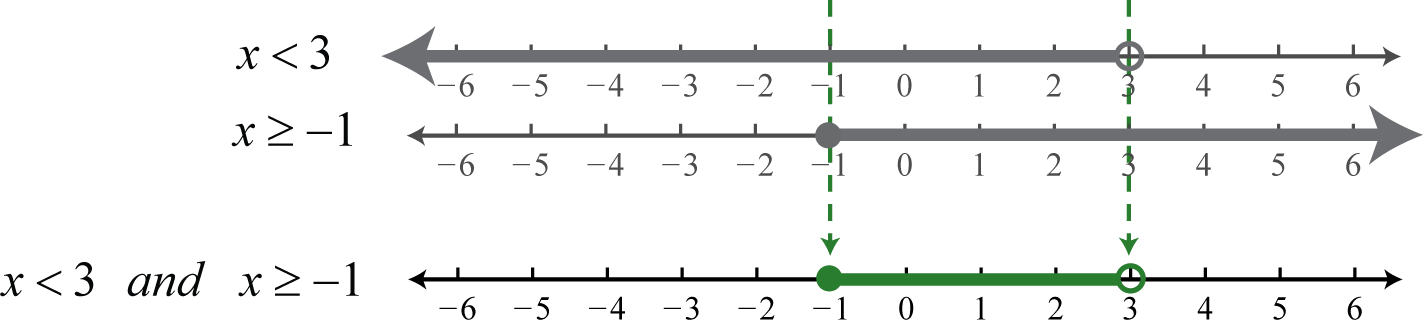
Hither, $3$ is not a solution considering it solves simply one of the inequalities. Alternatively, we may interpret $−1\leq x<3$ as all possible values for x between, or divisional by, $−1$ and $3$ where $−1$ is included in the solution ready.

Answer:

Interval note: $[\,−1, 3)$; prepare notation: $\{ten|−one\leq ten<iii\}$

Real Number Operations

Order of Operations

When we multiply a number by itself, we square it or enhance information technology to a power of $two$. For example, $4^two =iv\times4=16$. Nosotros can raise any number to any ability. In general, the exponential notation $a^due north$ ways that the number or variable $a$ is used as a gene $northward$ times.

\[a^n=a\cdot a\cdot a\cdots a \qquad \text{ n factors} \nonumber \]

In this notation, $a^n$ is read as the $due north^{thursday}$ power of $a$, where $a$ is called the base of operations and $n$ is called the exponent. A term in exponential note may be role of a mathematical expression, which is a combination of numbers and operations. For example, $24+6 \times \dfrac{2}{three} − 4^two$ is a mathematical expression.

To evaluate a mathematical expression, nosotros perform the various operations. However, nosotros practice not perform them in any random gild. We use the guild of operations. This is a sequence of rules for evaluating such expressions.

Remember that in mathematics nosotros use parentheses ( ), brackets [ ], and braces { } to group numbers and expressions then that annihilation actualization within the symbols is treated as a unit. Additionally, fraction bars, radicals, and accented value bars are treated as grouping symbols. When evaluating a mathematical expression, brainstorm by simplifying expressions inside group symbols.

The next footstep is to address whatsoever exponents or radicals. Afterward, perform multiplication and sectionalization from left to right and finally addition and subtraction from left to right.

Permit's take a await at the expression provided.

\[24+6 \times \dfrac{2}{three} − 4^two \nonumber\]

There are no grouping symbols, so motility on to exponents. The number $4$ is raised to a power of $2$, and then simplify $four^2$ equally $16$.

\[24+six \times \dfrac{ii}{three} − 4^two \nonumber \]

\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]

Next, perform multiplication or division, left to right.

\[24+6 \times \dfrac{2}{3} − 16 \nonumber\]

\[24+4-sixteen \nonumber\]

Lastly, perform addition or subtraction, left to correct.

\[24+4−16 \nonumber\]

\[28−xvi \nonumber\]

\[12 \nonumber\]

Therefore,

\[24+6 \times \dfrac{2}{3} − 4^2 =12 \nonumber\]

For some complicated expressions, several passes through the order of operations volition be needed. For instance, there may be a radical expression inside parentheses that must be simplified before the parentheses are evaluated. Following the order of operations ensures that anyone simplifying the same mathematical expression will go the aforementioned result.

ORDER OF OPERATIONS

Operations in mathematical expressions must be evaluated in a systematic lodge, which can be simplified using the acronym PEMDAS:

P(arentheses)
E(xponents)
M(ultiplication) and D(ivision)
A(ddition) and S(ubtraction)

$how-to.png$ How to: Given a mathematical expression, simplify information technology using the order of operations.

Simplify any expressions inside grouping symbols. Grouping symbols include parentheses ( ), brackets [ ], braces { }, fraction bars, radicals, and absolute value bars
Simplify any expressions containing exponents or radicals.
Perform any multiplication and partition in order, from left to right.
Perform any add-on and subtraction in social club, from left to right.

Case $\PageIndex{3}$: Using the Order of Operations

Use the social club of operations to evaluate each of the following expressions.

$(3+2)^2+four \times(vi+two)$
$\dfrac{five^two-4}{7}- \sqrt{11-2}$
$6−|five−8|+3\times(4−1)$ &&
$\dfrac{14-three \times2}{2 \times5-3^2}$
$7\times(5\times3)−2\times[(6−3)−four^ii]+1$

Solution

\[\begin{align*} (three\times2)^2-4\times(vi+ii)&=(6)^2-4\times(8) && \qquad \text{Simplify parentheses}\\ &=36-4\times8 && \qquad \text{Simplify exponent}\\ &=36-32 && \qquad \text{Simplify multiplication}\\ &=four && \qquad \text{Simplify subtraction}\\ \end{align*}\]
\[\brainstorm{align*} \dfrac{5^2-4}{7}- \sqrt{eleven-2}&= \dfrac{5^2-iv}{seven}-\sqrt{ix} && \qquad \text{Simplify grouping symbols }\\
&=\dfrac{5^2-4}{seven}-3 && \qquad \cdot \text{ radical: Subtract}\\
&=\dfrac{25-iv}{7}-three && \qquad \cdot \text{ numerator: Simplify exponent }\\
&=\dfrac{21}{vii}-3 && \qquad \cdot \text{ numerator: Subtract}\\
&=3-three && \qquad \text{Simplify division}\\
&=0 && \qquad \text{Simplify subtraction} \end{align*}\]

Note that in the first step, the radical is treated as a grouping symbol, like parentheses. Also, in the third step, the fraction bar is considered a grouping symbol and then the numerator is considered to be grouped.

\[\begin{align*} 6-\mid 5-8\mid +3\times(4-1)&=6-|-3|+iii\times3 && \qquad \text{Simplify inside group symbols}\\ &=6-3+three\times3 && \qquad \text{Simplify absolute value}\\ &=6-three+9 && \qquad \text{Simplify multiplication}\\ &=3+nine && \qquad \text{Simplify subtraction}\\ &=12 && \qquad \text{Simplify addition}\\ \cease{align*}\]
\[\begin{align*} \dfrac{14-3 \times2}{two \times5-3^2}&=\dfrac{fourteen-3 \times2}{2 \times5-9} && \qquad \text{Simplify exponent}\\ &=\dfrac{14-6}{10-9} && \qquad \text{Simplify products}\\ &=\dfrac{8}{one} && \qquad \text{Simplify differences}\\ &=eight && \qquad \text{Simplify caliber}\\ \stop{align*}\]

In this example, the fraction bar separates the numerator and denominator, which we simplify separately until the last stride.

\[\begin{align*} 7\times(5\times3)-2\times[(half-dozen-3)-4^2]+1&=7\times(15)-2\times[(3)-4^two]+1 && \qquad \text{Simplify inside parentheses}\\ &=seven\times(15)-2\times(three-sixteen)+i && \qquad \text{Simplify exponent}\\ &=7\times(15)-2\times(-13)+1 && \qquad \text{Subtract}\\ &=105+26+one && \qquad \text{Multiply}\\ &=132 && \qquad \text{Add} \terminate{align*}\]

$try-it.png$ Try Information technology $\PageIndex{3}$

Employ the order of operations to evaluate each of the following expressions.

$\sqrt{5^2-4^2}+seven\times(5-4)^2$
$1+\dfrac{vii\times5-8\times4}{9-6}$
$|1.8-4.iii|+0.four\times\sqrt{15+10}$
$\dfrac{1}{two}\times[5\times3^2-7^two]+\dfrac{ane}{3}\times9^two$
$[(iii-8^2)-4]-(3-8)$

Reply: a. $10$ $ \qquad $ b. $2$ $ \qquad $ c. $4.v$ $ \qquad $ d. $25$ $ \qquad $ eastward. $-60$

Real Number Properties

PROPERTIES OF REAL NUMBERS

The post-obit properties hold for real numbers $a$, $b$, and $c$.

	Addition	Multiplication
Commutative Property	$a+b=b+a$	$a\times b=b\times a$
Associative Property	$a+(b+c)=(a+b)+c$	$a(bc)=(ab)c$
Distributive Belongings	$a\times (b+c)=a\times b+a\times c$
Identity Property	There exists a unique real number called the additive identity, 0, such that, for any real number $a$ $a+0=a$	At that place exists a unique real number called the multiplicative identity, ane, such that, for any existent number $a$ $a\times 1=a$
Inverse Property	Every real number $a$ has an additive changed, or reverse, denoted $–a$, such that $a+(−a)=0$	Every nonzero existent number $a$ has a multiplicative changed, or reciprocal, denoted $\frac{i}{a}$ , such that $a\times \left(\dfrac{1}{a}\right)=1$

Constants and Variables

So far, the mathematical expressions we take seen take involved real numbers only. In mathematics, nosotros may come across expressions such as $x +v$, $\dfrac{4}{3}\pi r^3$, or $\sqrt{2m^3 north^2}$. In the expression $ten +5$, $5$ is called a abiding because information technology does non vary and $x$ is called a variable because it does. (In naming the variable, ignore any exponents or radicals included with the variable.) An algebraic expression is a collection of constants and variables joined together by the algebraic operations of addition, subtraction, multiplication, and division.

Example $\PageIndex{4}$: Describing Algebraic Expressions

List the constants and variables for each algebraic expression.

a. $x + v$

b. $\dfrac{iv}{3}\pi r^3$

c. $\sqrt{2m^3 n^2}$

Solution

	a. $x + 5$	b. $\dfrac{four}{three}\pi r^3$	c. $\sqrt{2m^3 n^2}$
Constants	$5$	$\dfrac{4}{three}$, $\pi$	$2$
Variables	$10$	$r$	$m$, $due north$

$try-it.png$ Try It $\PageIndex{4}$

List the constants and variables for each algebraic expression.

$2\pi r(r+h)$
$ii(L + West)$
$4y^3+y$

Respond

	a. $2\pi r(r+h)$	b. $ii(Fifty + W)$	c. $4y^iii+y$
Constants	$ii$,$\pi$	$ii$	$iv$
Variables	$r$,$h$	$L$, $Westward$	$y$

Evaluating Algebraic Expressions

We have already seen some real number examples of exponential note, a shorthand method of writing products of the same gene. When variables are used, the constants and variables are treated the same way.

\[\begin{align*} (-3)^5 &=(-iii)\times(-3)\times(-3)\times(-3)\times(-3)\Rightarrow 10^5=x\times 10\times x\times x\times ten\\ (2\times7)^iii&=(2\times7)\times(2\times7)\times(2\times7)\qquad \; \; \quad \Rightarrow (yz)^3=(yz)\times(yz)\times(yz) \end{marshal*}\]

In each case, the exponent tells us how many factors of the base to use, whether the base of operations consists of constants or variables.

Any variable in an algebraic expression may take on or be assigned dissimilar values. When that happens, the value of the algebraic expression changes. To evaluate an algebraic expression means to decide the value of the expression for a given value of each variable in the expression. Replace each variable in the expression with the given value, then simplify the resulting expression using the social club of operations. Parentheses should be used to avoid ambivalence. If the algebraic expression contains more than one variable, replace each variable with its assigned value and simplify the expression equally before.

Instance $\PageIndex{5}$: Evaluating an Algebraic Expression at Dissimilar Values

Evaluate the expression $2x−7$ for each value for $ten$.

$x=0$
$x=one$
$x=12$
$x=−4$

Solution

Substitute $0$ for $ten$. $ \quad 2x-seven = 2(0)-7 = 0-vii= -7 $
Notice if parentheses were non used, $2(0)$ would have been $xx$, which is wrong!!!
Substitute $i$ for $x$. $ \quad2x-seven = 2(1)-vii= two-7= -5 $
Substitute $\dfrac{1}{ii}$ for $10$. $ \quad 2x-7 = ii\left (\dfrac{1}{two} \right )-7 = 1-7= -6 $
Substitute $-four$ for $x$. $ \quad 2x-vii = ii(-4)-vii= -8-7= -15 $
Discover if parentheses were not used, $2(-4)$ which is $-6$, would accept been \2 - 4\) or $-two$, which is incorrect!!!

ALWAYS apply parentheses in situations where not using them would create an incorrect expression!

$try-it.png$ Attempt It $\PageIndex{5}$

Evaluate the expression $eleven−3y$ for each value for $y$.

$y=two$
$y=0$
$y=\dfrac{2}{iii}$
$y=−v$

Respond: a. $v$ $ \qquad$ b. $11$$ \qquad$ c. $9$$ \qquad$ d. $26$

Case $\PageIndex{6}$: Evaluating Algebraic Expressions

Evaluate each expression for the given values.

$x+5$ for $x=-5$
$\dfrac{t}{2t-1}$ for $t=ten$
$\dfrac{4}{3}\pi r^3$ for $r=5$
$a+ab+b$ for $a=eleven$ , $b=-eight$
$\sqrt{2m^3 northward^2}$ for $m=2$ , $n=3$

Solution

$-five$ for $10$. \[\begin{marshal*} 10+5 &= (-5)+v = 0\\ \finish{align*}\]
Substitute $10$ for $t$. \[\begin{marshal*} \dfrac{t}{2t-1} &= \dfrac{(10)}{2(10)-one} \\ &= \dfrac{ten}{xx-one}= \dfrac{10}{nineteen}\\ \end{align*}\]
Substitute $5$ for $r$. \[\begin{align*} \dfrac{4}{three} \pi r^iii &= \dfrac{4}{3}\pi (5)^iii \\ &= \dfrac{iv}{3}\pi (125)= \dfrac{500}{iii}\pi\\ \end{marshal*}\]
Substitute $eleven$ for $a$ and $-8$ for $b$. \[\begin{marshal*} a+ab+b &= (11)+(11)(-viii)+(-8) \\ &= 11-88-8 = -85\\ \stop{align*}\]
Substitute $ii$ for $chiliad$ and $3$ for $n$. \[\begin{marshal*} \sqrt{2m^3 due north^two} &= \sqrt{2(ii)^three (3)^2} \\ &= \sqrt{two(8)(9)} \\ &= \sqrt{144} = 12 \terminate{align*}\]

$try-it.png$ Attempt It $\PageIndex{6}$

Evaluate each expression for the given values.

$\dfrac{y+3}{y-3}$ for $y=5$
$7-2t$ for $t=-two$
$\dfrac{1}{3}\pi r^two$ for $r=eleven$
$(p^2 q)^three$ for $p=-2$, $q=iii$
$iv(thou-n)-5(northward-m)$ for $k=\dfrac{2}{3}$ $due north=\dfrac{1}{iii}$

Answer: a. $4$ $ \qquad$ b. $11$ $ \qquad$ c. $\dfrac{121}{3}\pi$ $ \qquad$ d. $1728$ $ \qquad$ east. $3$

Simplifying Algebraic Expressions

Sometimes we can simplify an algebraic expression to make it easier to evaluate or to use in another style. To do so, we utilize the properties of real numbers. We tin utilise the aforementioned properties in formulas because they incorporate algebraic expressions.

Example $\PageIndex{vii}$: Simplifying Algebraic Expressions

Simplify each algebraic expression.

$3x-2y+x-3y-seven$
$2r-five(3-r)+4$
$\left(4t-\dfrac{5}{4}s\right)-\left(\dfrac{2}{three}t+2s\right)$
$2mn-5m+3mn+n$

Solution

\[\begin{marshal*} 3x-2y+10-3y-vii&=3x+x-2y-3y-7 && \qquad \text{Commutative property of addition}\\ &=4x-5y-7 && \qquad \text{Simplify}\\ \end{align*}\]
\[\begin{align*} 2r-5(3-r)+four&=2r-15+5r+four && \qquad \qquad \qquad \text {Distributive property}\\ &=2r+5r-15+four && \qquad \qquad \qquad \text{Commutative property of improver}\\ &=7r-xi && \qquad \qquad \qquad \text{Simplify}\\ \terminate{align*}\]
\[\begin{align*} \left(4t-\dfrac{v}{4}s\right)-\left(\dfrac{2}{3}t+2s\right)&=4t-\dfrac{5}{4}s-\dfrac{2}{3}t-2s && \qquad \text{Distributive property}\\ &=4t-\dfrac{2}{3}t-\dfrac{5}{iv}s-2s && \qquad \text{Commutative property of add-on}\\ &=\dfrac{10}{3}t-\dfrac{13}{4}s && \qquad \text{Simplify}\\ \cease{align*}\]
\[\begin{align*} 2mn-5m+3mn+n&=2mn+3mn-5m+n && \qquad \text{Commutative property of improver}\\ &=5mn-5m+n && \qquad \text{Simplify} \end{align*}\]

$try-it.png$ Effort It $\PageIndex{vii}$

Simplify each algebraic expression.

$\dfrac{2}{3}y−two\left(\dfrac{4}{3}y+z\correct)$
$\dfrac{five}{t}−2−\dfrac{3}{t}+1$
$4p(q−1)+q(1−p)$
$9r−(s+2r)+(half dozen−s)$

Answer: a. $−2y−2z$ or $−two(y+z)$ $ \qquad$ b. $\dfrac{2}{t}−1$ $ \qquad$c. $3pq−4p+q$ $ \qquad$d.$7r−2s+half dozen$

Example $\PageIndex{viii}$: Simplifying a Formula

A rectangle with length $L$ and width $Westward$ has a perimeter $P$ given by $P =L+W+50+Due west$ . Simplify this expression.

Solution

\[\begin{align*} P &=50+W+L+Due west\\ P &=L+L+W+W && \qquad \text{Commutative belongings of addition}\\ P &=2L+2W && \qquad \text{Simplify}\\ P &=2(L+W) && \qquad \text{Distributive belongings} \end{marshal*}\]

$try-it.png$ Try It $\PageIndex{viii}$

If the amount $P$ is deposited into an account paying elementary interest $r$ for fourth dimension $t$ , the total value of the deposit $A$ is given by $A =P+Prt$ . Simplify the expression. (This formula will be explored in more item afterwards in the course.)

Answer: $A=P(1+rt)$

Glossary

algebraic expression: constants and variables combined using add-on, subtraction, multiplication, and division

associative property of add-on: the sum of iii numbers may be grouped differently without affecting the effect; in symbols, a+(b+c) = (a+b)+c

associative holding of multiplication: the production of 3 numbers may be grouped differently without affecting the result; in symbols, a(bc) = (ab)c

base: in exponential notation, the expression that is being multiplied

commutative belongings of addition: two numbers may be added in either order without affecting the event; in symbols, a + b = b + a

commutative holding of multiplication: two numbers may be multiplied in any guild without affecting the effect; in symbols, ab = ba

abiding: a quantity that does not alter value

distributive property: the product of a factor times a sum is the sum of the gene times each term in the sum; in symbols, a(b+c) = ab + ac

equation: a mathematical argument indicating that ii expressions are equal

exponent: in exponential note, the raised number or variable that indicates how many times the base is existence multiplied

exponential notation: a shorthand method of writing products of the same gene

formula: an equation expressing a human relationship betwixt constant and variable quantities

identity property of addition: in that location is a unique number, called the additive identity, 0, which, when added to a number, results in the original number; in symbols, a + 0 = a

identity property of multiplication: there is a unique number, called the multiplicative identity, i, which, when multiplied past a number, results in the original number; in symbols, $ a \cdot 1 = a$

integers: the set consisting of the natural numbers, their opposites, and 0: { ... -3, -two, -1, 0, 1, ii, 3, ... }

inverse property of addition: for every real number $a$ at that place is a unique number, chosen the additive changed (or opposite), denoted $-a$; which, when added to the original number, results in the additive identity, 0; in symbols, $ a + (-a) = 0 $

inverse property of multiplication: for every non-goose egg real number $a$ there is a unique number, called the multiplicative inverse (or reciprocal), denoted $ \frac{ane}{a} $ which, when multiplied by the original number, results in the multiplicative identity, i; in symbols $ a \cdot \frac{1}{a} = i$.

irrational numbers: the set of all numbers that are non rational; they cannot exist written every bit either a terminating or repeating decimal; they cannot be expressed as a fraction of two integers

natural numbers: the prepare of counting numbers: {1, ii, 3, ...}.

order of operations: a set of rules governing how mathematical expressions are to be evaluated, assigning priorities to operations

rational numbers: the set of all numbers of the class $\frac{m}{n}$ where $thousand$ and $northward$ are integers and $due north \ne 0$. Any rational number may be written equally a fraction or a terminating or repeating decimal.

real number line: a horizontal line used to correspond the real numbers. An arbitrary fixed point is chosen to represent 0; positive numbers lie to the correct of 0 and negative numbers to the left.

existent numbers: the sets of rational numbers and irrational numbers taken together

variable: a quantity that may change value

whole numbers: the set consisting of 0 plus the natural numbers: {0, 1, 2, 3, ...}.